Spring Mass Dashpot System

A structure is modelled as the spring-mass-dashpot system shown below. For such a system is its natural frequency of vibration. When you see this kind of spring-mass system each Mass is the building block of the system. The force is considered to be proportional the instantaneous velocity. Newtons law gives mx00 ky x bx0 or putting the system on the left and the driving term on the right mx00bx0kx ky. The spring exerts a force given by ky x where k is the spring constant and the dashpot exerts a force given by bx0 against the motion of the mass with damping coefficient b. Only horizontal motion and forces are considered.

This model is well-suited for modelling object with complex material properties such as nonlinearity and viscoelasticity.

0- 0 10 20 30 40 50 a xt Type an exact answer. We assume that x0 when the spring is in its. The left hand side represents the SYSTEM the springmassdashpot system. A spring of length l has a mass m attached to it and a dashpot damping the motion. An external force is also shown. So the di erential equation for the mass spring is now m d2x dt2 kx dx zdt friction force.

Spring Mass Damper System 1dof Youtube

Spring mass dashpot system. If a spring-mass-dashpot system is subjected to excitation by a constant harmonic force then at resonance its amplitude of vibration will be IES-1999 a infinity b inversely proportional to damping c directly proportional to damping d decreasing exponentially with time 23. Now we consider a mass on a spring in which there is friction. We will consider three types of forcing applied to the spring-mass system as shown below.

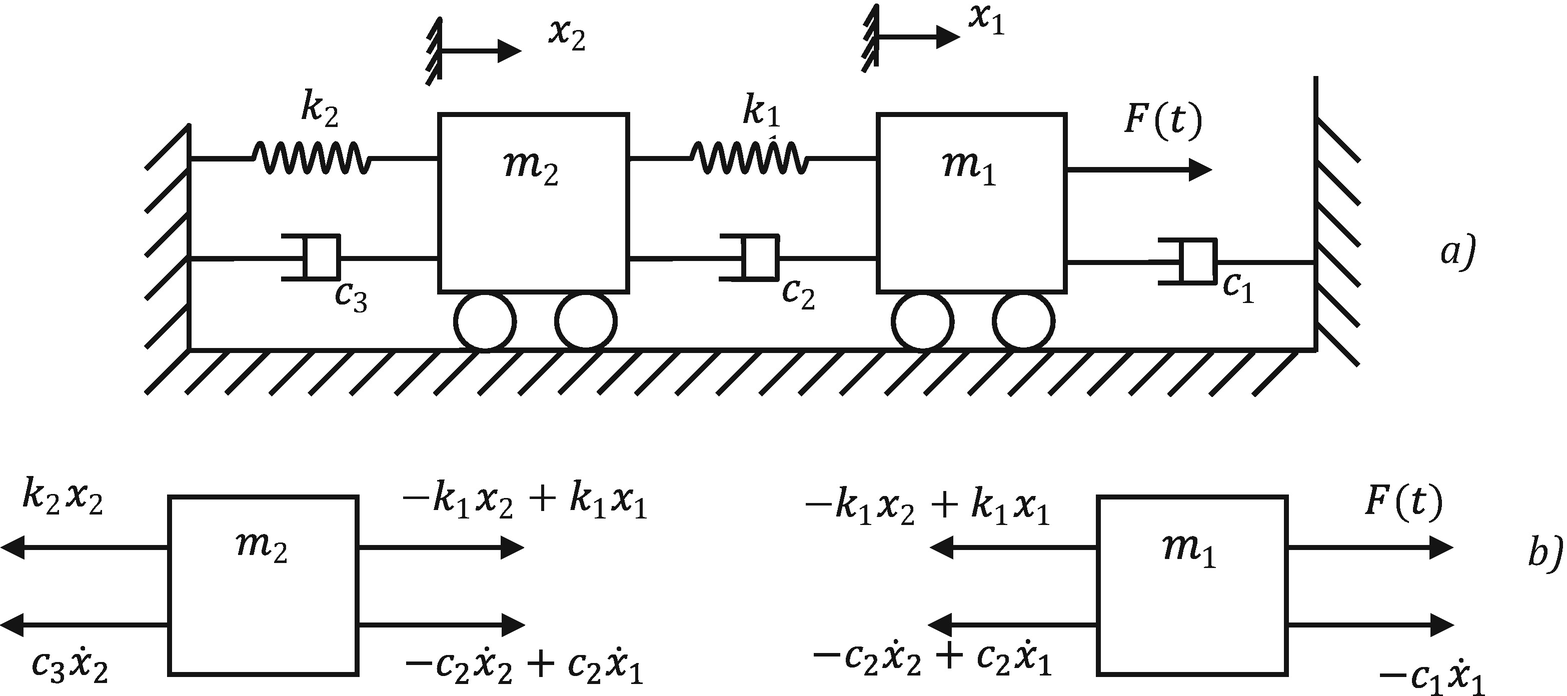
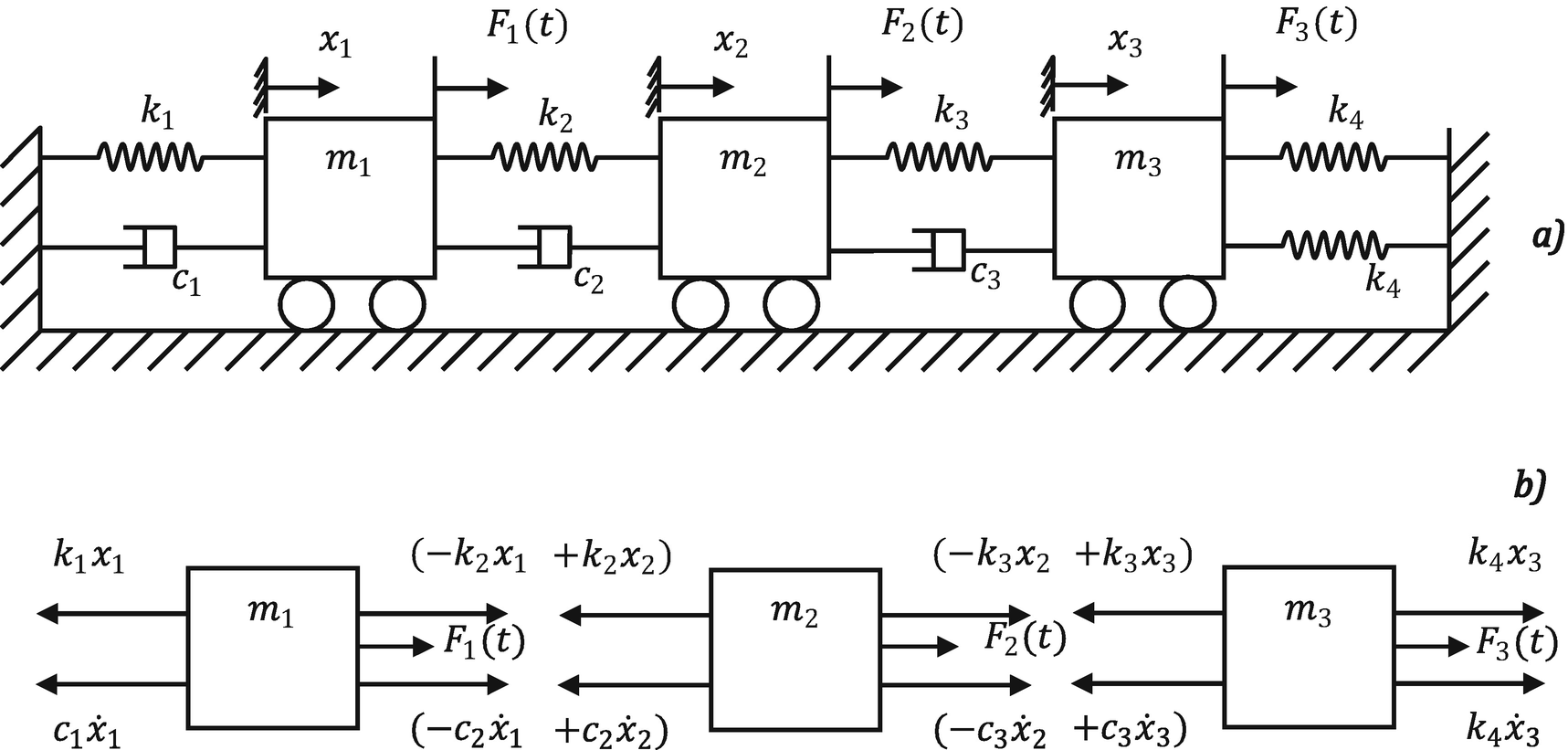
A mass spring dashpot subsystem in a falling container of mass m 1 is shown. There is only one position in this system defined by the variable x that is positive to the right. Ii Draw the arrows vectors to represent the direction of Forces being applied to each component.

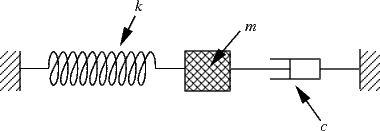
Another common misconception is that the model shown in Figure 12 is re-lated to only a particular physical system which consists of a lumped mass attached to a tension-compression spring with a dashpot acting in paral-lel. Spring elastic element Damper frictional element Mass inertia element Translational and rotational versions These are passive non-energy producing devices Driving Inputs force. The coefficients represent parameters of the system -- for example mass damping constant spring constant.

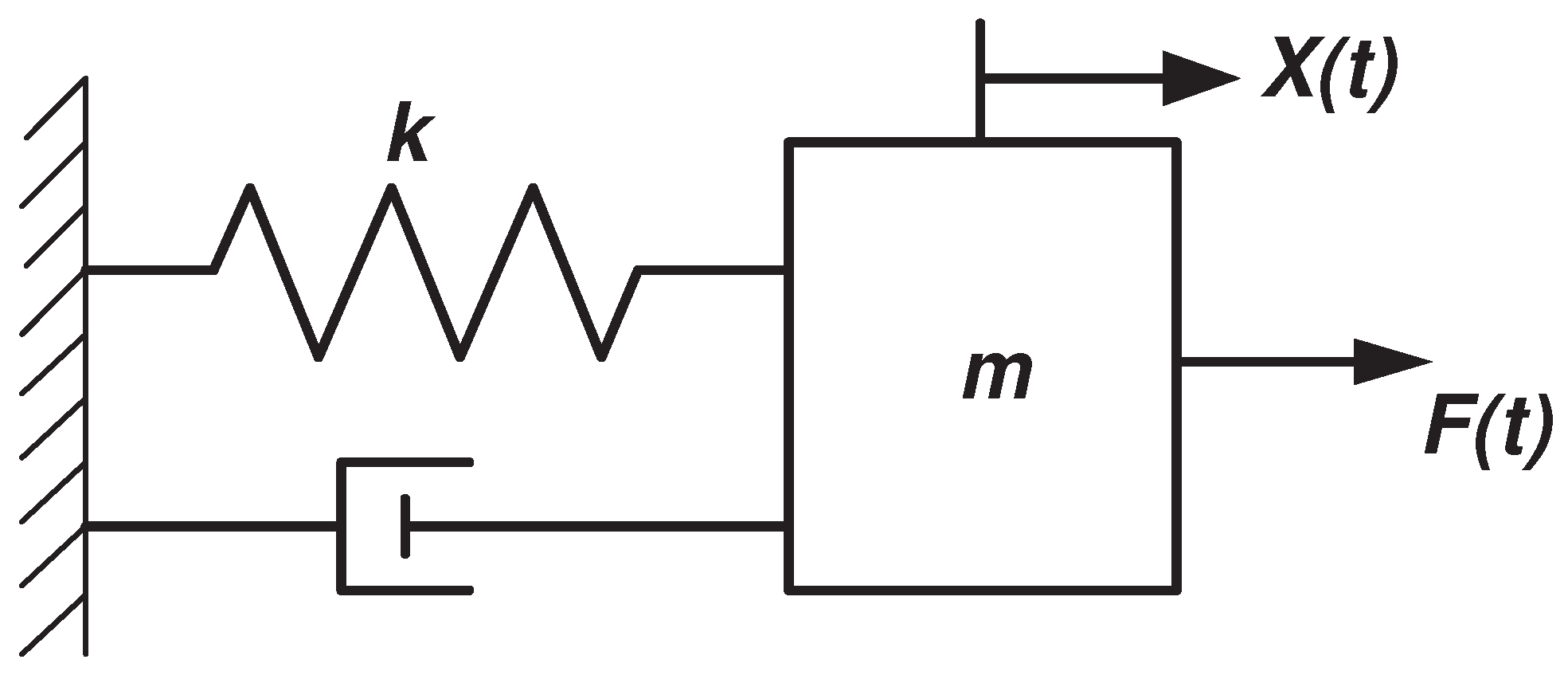
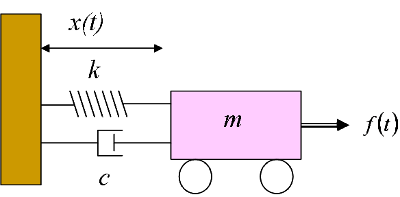
The spring exerts a force given by ky x where k is the spring constant and the dashpot exerts a force given by bx0 against the motion of the mass with damping coefficient b. The system is subject to constraints not shown that confine its motion to the vertical direction only. The spring friction between the mass and the guides if any that constrain its motion to one dimension or a mechanical device dashpot that imparts a resistive force to the mass.

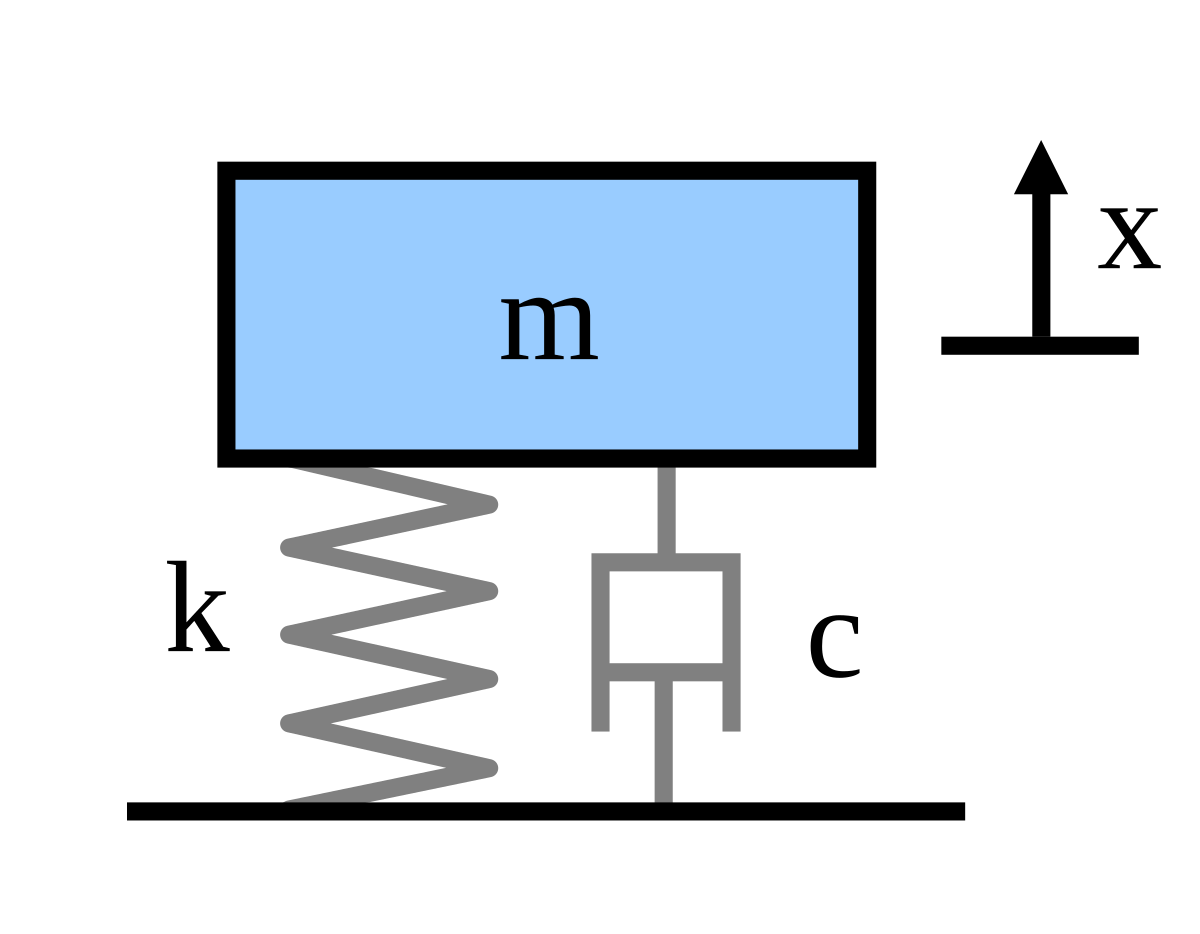
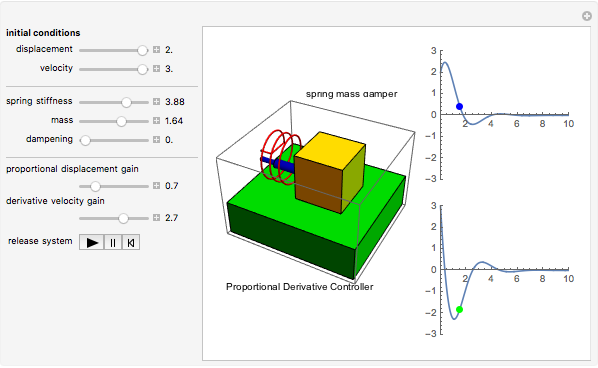
The basic vibration model of a simple oscillatory system consists of a mass a massless spring and a damper. A structure is modelled as the spring-mass-dashpot system shown below. Suppose that the mass in a mass-spring-dashpot system with m 10 c 7 and k 1 is set in motion with x0 0 and x0 5.

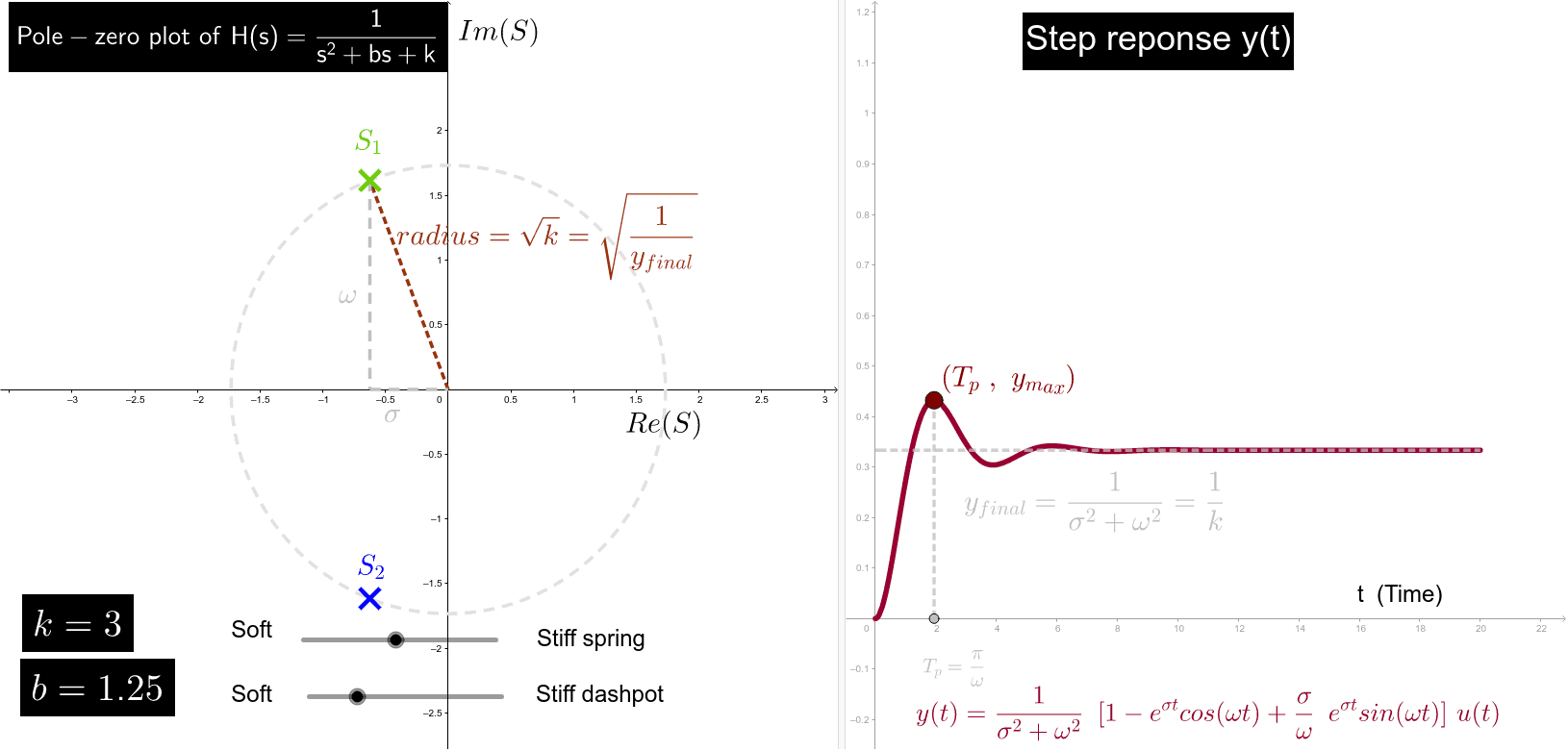
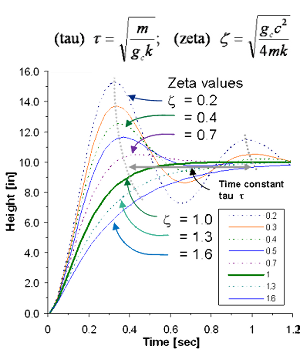
A Determine the natural frequency of the undamped system in both rads and Hz and its natural period. In any case we assume that the resistive force is proportional to the speed dudtof the mass. For such a system is its natural frequency of vibration.

B Given the damping coefficient c calculate the damping ratio. I Break down the system into each component.

Entropy Free Full Text Modeling Of A Mass Spring Damper System By Fractional Derivatives With And Without A Singular Kernel

A Spring Mass Damper System Subjected To Base Excitation Download Scientific Diagram

1 Spring Mass Damper System Download Scientific Diagram

Free Vibrations Of A Spring Mass Damper System Wolfram Demonstrations Project

Dsc Mass Spring Damper Concept Youtube

Mass Spring Damper Model Wikipedia

301 Vibration Of Mass Spring Damper System Memorandums Of A Novice Automotive Engineer

Obtaining Steady State Solution For Spring Mass Dashpot System Stack Overflow

Mass Spring Damper System

Solved Problem 1 Consider The Spring Mass Damper System Chegg Com

Control Of A Spring Mass Damper System Using Mixed Mu Synthesis Matlab Simulink Example Mathworks America Latina

A Sdof Mass Spring Damper System Download Scientific Diagram

File Mass Spring Damper Svg Wikipedia

Restackor Spring Mass Damper Theory

Drawing Mechanical Systems Mass Damper Spring In Latex Tex Latex Stack Exchange

Spring Mass Damper Systems Springerlink

File Mass Spring Damper System Phase Plane Nodal Sink Gif Wikimedia Commons

Modeling A Mass Spring Damper System Physics Forums

3 Mass Spring Damper System Acted On By An Excitation Function Download Scientific Diagram

1dof Spring Mass Damper System By Michael Alletto Openfoam Wiki

Equation Generation Mass Spring Damper Multibody Multi Domain Physical Model In Maplesim Maplesoft

Compute The Damping Value For Two Masses In A Harmonic Oscillator Physics Stack Exchange

Um Ma216 Demos 3 4 Spring

1

Spring Mass Damper Matlab Ode Solver Youtube

Solved Q2 The Following Is A Spring Mass Damper System The Chegg Com

1 There Is A Mass Spring Damper System As Shown In Fig 1 A Find The Total Response X T In Homeworklib

Spring Mass Damper Systems Springerlink

Consider The Spring Mass Damper System Mounted On A Massless Cart As Shown In The Figure Below In This System U T Is The Displacement Of The Cart And Is The Input To The System

State Space Representation Of A Mass Spring Damper System The Robotics Lab

How To Model A Simple Spring Mass Damper Dynamic System In Matlab 12 Steps Instructables

Mass Spring Damper Model Wikipedia

Double Mass Spring Damper System Download Scientific Diagram

Initialize Variables For A Mass Spring Damper System Matlab Simulink Mathworks Espana

File Spring Mass Damper System Svg Wikimedia Commons

Mass Spring Damper Draw Claytex

Mass Spring Damper Tutorial Youtube

Solved Problem 2 Consider The Following Spring Mass Damper Chegg Com

Mass Damper An Overview Sciencedirect Topics

Step Response Of A Spring Mass Dashpot System Geogebra

Mass Spring Damper In Simulink And Simscape Skill Lync

Spring Mass Damper Smd System With Proportional Derivative Pd Controller Wolfram Demonstrations Project

Mass Spring Damper System For An Example Modeling Problem Download Scientific Diagram

Solved In The Spring Mass Damper System Shown The Block Slides With No 2 Answers Transtutors

Restackor Spring Mass Damper Theory

Tuned Mass Dampers Flow Engineering

Linear Mass Spring Damper With Gravity Pydy Distribution 0 6 0 Dev0 Documentation

Spring Mass Damper System 2dof Youtube

1

There are two forces acting on the mass.

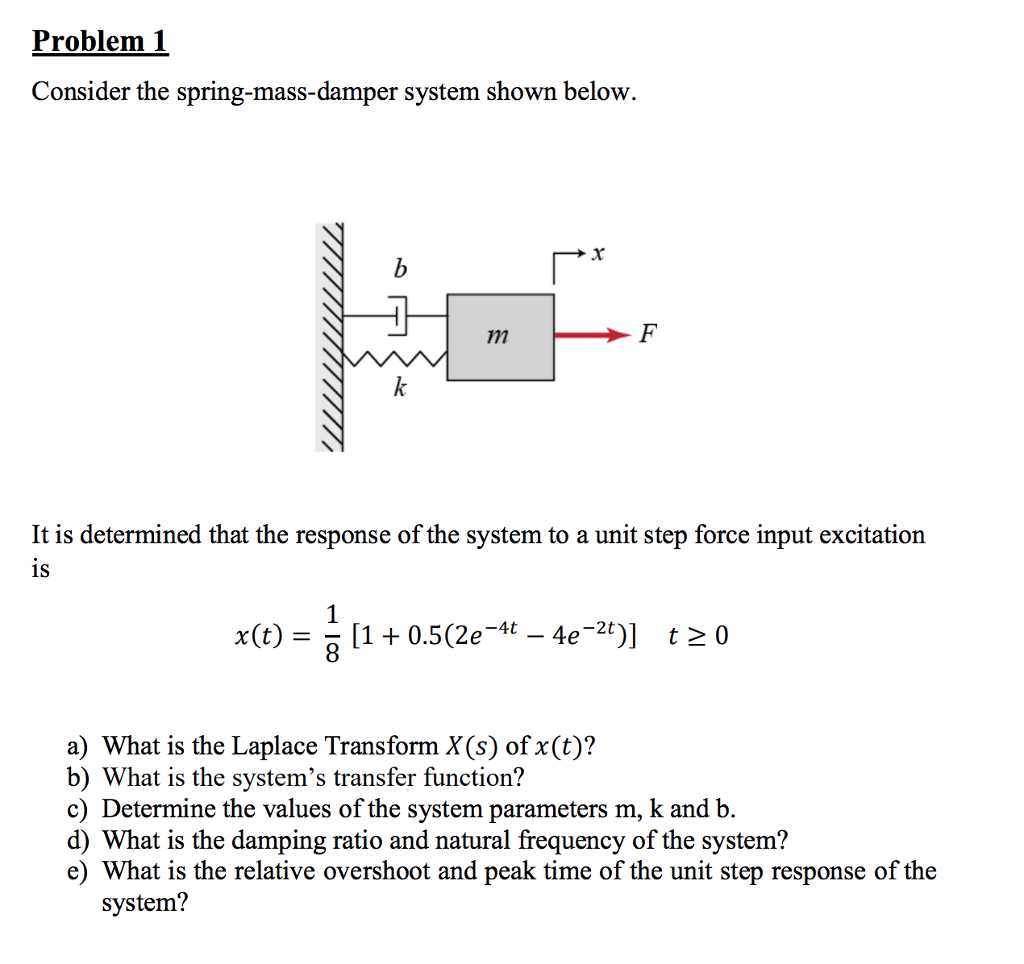
It is subject to a force f t forcing the motion as in Figure 142. Now we consider a mass on a spring in which there is friction. A mass spring dashpot subsystem in a falling container of mass m 1 is shown. The spring exerts a force given by ky x where k is the spring constant and the dashpot exerts a force given by bx0 against the motion of the mass with damping coefficient b. The system can then be considered to. The basic vibration model of a simple oscillatory system consists of a mass a massless spring and a damper. B Given the damping coefficient c calculate the damping ratio. A Find the position function xt and show that its graph looks as indicated in the figure. So the di erential equation for the mass spring is now m d2x dt2 kx dx zdt friction force.

A mass spring dashpot subsystem in a falling container of mass m 1 is shown. The mass could represent a car with the spring and dashpot representing the cars bumper. The frequency-dependent spring and dashpot properties are generated by a FORTRAN program using the basic model constants for the mass m and for the spring In addition the parameters b138366 23508 в 10 2 and 65001 в 10 2 are used. B Find how far the mass moves to the right before starting back toward the origin. This discussion on If a spring-mass-dashpot system is subjected to excitation by a constant harmonic force then at resonance its amplitude of vibration will be aInfinitybInversely proportional to damp in cDirectly proportional to dampingdDecreasing exponentially with timeCorrect answer is option A. Spring elastic element Damper frictional element Mass inertia element Translational and rotational versions These are passive non-energy producing devices Driving Inputs force. 6 In this example it is natural to regard y rather than the right.